Example 1431 Calculating Partial Derivatives from the Definition Use the definition of the partial derivative as a limit to calculate ∂ f / ∂ x and ∂ f / ∂ y for the function f(x, y) = x2 − 3xy 2y2 − 4x 5y − 12 Solution First, calculate f(x h, y) f(x h, y) = (x h)2 − 3(x h)y 2y2 − 4(x h) 5y − 12Answer (1 of 2) This question is meaningless as you only define partial derivatives of a function f of more than one variables with respect to one of the specific variables among them If your function is given by f(x,y) = x for all (x,y), then (del f)/(del y) = 0, everywhere if the variable x∂y x,z in the first, x, y, t are the independent variables;

Using Nabla With Partial Derivatives And The Laplace Operation Partial X 2 Partial Y 2 Partial Z 2 Mathematics Stack Exchange
X/(x^2 y^2) partial derivative
X/(x^2 y^2) partial derivative- Hayate 1 0 SOLVED The partial derivatives of arctan (y/x) let w = arctan (y/x) the partial derivatives are dw/dx and dw/dy i know that the derivative or arctan (x) is 1/ (1x^2) so for dw/dy, i get (1/ 1 (y^2/x^2) ) * (1/x) = x/ (x^2 y^2) ???Generalizing the second derivative Consider a function with a twodimensional input, such as Its partial derivatives and take in that same twodimensional input Therefore, we could also take the partial derivatives of the partial derivatives These are called second partial derivatives, and the notation is analogous to the notation for




Answered Find The Partial Derivatives With Bartleby
@x is read as \partial derivative of z (or f) with respect to x", and means difierentiate with respect to x holding y constant † @z @y means difierentiate with respect to y holding x constant Another common notation is the subscript notation zx means @z @x zy means @z @y Note that we cannot use the dash 0 symbol for partial difierentiation because it would not be clear what we areY0 z0) = d dx f x y0 z0 lim h!Approximate partial derivatives from a table If the average value of f on the interval 2 to 4 is 3, then find the integral shown Find the partial derivatives of f (x,y,z)=xyz Find the partial derivatives of f (x,y,z)=xyz Find and interpret the partial derivatives of f (x,y)=3x2y4
Get stepbystep solutions from expert tutors as fast as 1530 minutes We have y = ln(x^2y^2) Method 1 Implicit differentiation, as is Using the chain rule dy/dx = 1/(x^2y^2)(2x2ydy/dx) " " = (2x)/(x^2y^2) (2y)/(x^2y^2)dy/dxY0 z0), the value of the partial derivative with respect to x is (161) ∂f ∂x (x0;
Partial Derivative Formulas and Identities There are some identities for partial derivatives as per the definition of the function 1 If u = f (x,y) and both x and y are differentiable of t ie x = g (t) and y = h (t), then the term differentiation becomes total differentiation 2To apply the implicit function theorem to find the partial derivative of y with respect to x 1 (for example), first take the total differential of F dF = F ydy F x 1 dx 1 F x 2 dx 2 =0 then set all the differentials except the ones in question equal to zero (ie set dx 2 =0)which leaves F ydy F x1 dx 1 =0 or F ydy = −F x 1 dx 1 dividing both sides by F y and dx 1 yields dy dx 1 = −{eq}f(x,y)=\frac{1}{\sqrt{x^{2}y^{2}}} {/eq} Partial Derivative The derivative of the composition of two or more variables with respect to one taking other as the constant is known as the partial




Solved Find All The Second Order Partial Derivatives Of The Chegg Com



Partial Derivatives
Likewise the partial derivative \({f_y}\left( {a,b} \right)\) is the slope of the trace of \(f\left( {x,y} \right)\) for the plane \(x = a\) at the point \(\left( {a,b} \right)\) Example 2 Find the slopes of the traces to \(z = 10 4{x^2} {y^2}\) at the point \(\left( {1,2} \right)\) Show Solution We sketched the traces for the planes \(x = 1\) and \(y = 2\) in a previous section andThat is, the order in which the derivatives are taken in the mixed partials is immaterial Example 1 If ƒ ( x, y) = 3 x 2 y 5 x − 2 y 2 1, find ƒ x, ƒ y, ƒ xx, ƒ yy, ƒ xy 1, and ƒ yx First, differentiating ƒ with respect to x (while treating y as a constant) yields There's a factor of 2 missing in all your second derivatives The result is exactly as you'd expect The variable you're differentiating with respect to, matters If it's x, then y is treated as a constant, and vice versa So if the "active" variable is leading in the numerator in one derivative, the same should apply in the other



Partial Derivatives



Ualberta Ca
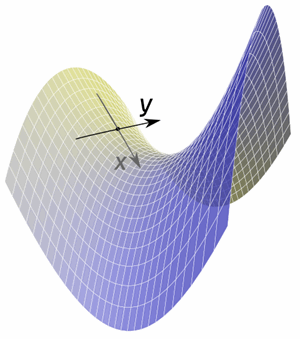
Partial derivative of x^2y^2/ (x^2y^2) \square!PoyffffIfn n x and y B Partial derivative nfwrtX cxy is É x y s fx x y s his fathiffad if limit exists rate which f o's as we vary x holding y fixed Fix y define gox fax y then j Y't y If ix y s dy x iii To compute If regard y as constant differentiate w r t to x Y is defined and computed similarly Let f be a fan n x y and z Partials are defined similarly Second partial derivative 3 2,1 s HowA graph of z = x 2 xy y 2 For the partial derivative at (1, 1) that leaves y constant, the corresponding tangent line is parallel to the xzplane A slice of the graph above showing the function in the xzplane at y = 1 Note that the two axes are shown here with different scales The slope of the tangent line is 3 The graph of this function defines a surface in Euclidean space To



1




Solved Chapter 14 Section 14 7 Question 007 Your Answer Is Partially Correct Try Again Calculate All Four Second Order Partial Derivatives And Check That Fxy Fyx Assume The Variables Are Restricted To Domain On
0 f (x0 h;Partial derivative of exp(x^2 y^2) Natural Language;Derivative of x/(x^2y^2) by x = (y^2x^2)/(y^42*x^2*y^2x^4) Show a step by step solution;



Compute Partial Derivatives Of The Given Function Stumbling Robot



Users Math Msu Edu
Then the x2 y2 z z tangent plane is z = z0 0 x0 (x−x y0 x0 x y0 y , since x2y2 = z2 0) (y−y0), or z = z0 z0 z0 z0 b) The line is x = x0t, yGiven below are some of the examples on Partial Derivatives Question 1 Determine the partial derivative of a function f x and f y if f (x, y) is given by f (x, y) = tan (xy) sin x Solution Given function is f (x, y) = tan (xy) sin x Derivative of a function with respect to xIterated Derivative Notations Let f (x, y) = x2y3 There are two notations for partial derivatives, f x and @f @x Partial derivative of f with respect to x in each notation f x = 2xy3 @ @x f (x, y) = @f @x = 2xy3 Partial derivative of that with respect to y ( f x) y = f xy, @ @y @ @x f = @2 @y @x f so f xy(x, y) = 6xy2 = @2f @y @x = 6xy2 Notice derivatives are listed in the opposite order




Solved A Find The Partial Derivatives Partial Differential Chegg Com




Partial Derivatives Calculus 3
∂y Key Point 2 The Partial Derivative of f with respect to y For a function of two variables z = f(x,y) the partial derivative of f with respect to y is denoted by ∂f ∂y and is obtained by differentiating f(x,y) with respect to y in the usual way but treating the xvariable as if it were a constant Alternative notations for ∂f ∂y are f y(x,y) or f y or ∂z ∂y 10 HELM (08 In this case we call h′(b) h ′ ( b) the partial derivative of f (x,y) f ( x, y) with respect to y y at (a,b) ( a, b) and we denote it as follows, f y(a,b) = 6a2b2 f y ( a, b) = 6 a 2 b 2 Note that these two partial derivatives are sometimes called the first order partial derivatives Just as with functions of one variable we can haveWe take the first equation {eq}x^2 y^2 w^2 z^2 = 1 {/eq} and take the partial derivative wrt x with z as a constant, as denoted in the See full answer below




Solved Find The Partial Derivative Of F X Y E X2 Y2 With Chegg Com



Partial Derivatives
PARTIAL DERIVATIVE LINKSImplicit differentiation Partial derivative (i) y cos x = x^2y^2 (ii) e^z = xyz https//youtube/N6TLvbDCOUkLagrange's MultipX and z held constant";Log in Linda H Numerade Educator Like Report Jump To Question Problem 1 Problem 2 Problem 3 Problem 4 Problem 5 Problem 6 Problem 7 Problem 8 Problem 9 Problem 10 Problem 11 Problem 12 Problem 13 Problem 14 Problem 15 Problem 16 Problem 17 Problem 18 Problem 19 Problem



Ualberta Ca




Solved Find All The First Order Partial Derivatives For The Chegg Com
f x ( x 0, y 0) ( x − x 0) f y ( x 0, y 0) ( y − y 0) f ( x 0, y 0) is the z value of the point on the plane above ( x, y) Equation 1431 says that the z value of a point on the surface is equal to the z value of a point on the plane plus a "little bit,'' namely ϵ 1 Δ x ϵ 2 Δ yThe partial derivative of a function of multiple variables is the instantaneous rate of change or slope of the function in one of the coordinate directions Computationally, partial differentiation works the same way as singlevariable differentiation with all other variables treated as constant The partial derivative of a function f (x, y) f(x,y) f (x, y) in the x x xdirection can beLet's first think about a function of one variable (x) f(x) = x 2 We can find its derivative using the Power Rule f'(x) = 2x But what about a function of two variables (x and y) f(x, y) = x 2 y 3 We can find its partial derivative with respect to x when we treat y as a constant (imagine y is a number like 7 or something) f' x = 2x 0 = 2x




Use The Chain Rule To Find The Partial Derivative Ofth Itprospt



Find The Partial Derivatives Of The Following Functions At The Indicated Points I F X Y 3x 2 2xy Y 2 5x 2 2 5 Sarthaks Econnect Largest Online Education Community
For virtually all functions ƒ ( x, y) commonly encountered in practice, ƒ vx;Find the indicated partial derivative $ f(x, y, 08 View Full Video Already have an account?By symmetry (interchanging x and y), zy = ;




Partial Derivative Math Help Forum



Derivative Calculator With Steps
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!We will need two quantities to classify the critical points of f(x,y) 1 f xx, the second partial derivative of f with respect to x 2 H = f xxf yy −f2 xy the Hessian If the Hessian is zero, then the critical point is degenerate If the Hessian is nonzero, then the critical point is nondegenerate and we can classify the points in the following manner case(i) If H > 0 and f xx < 0 thenDefinition of Partial Derivatives Let f(x,y) be a function with two variables If we keep y constant and differentiate f (assuming f is differentiable) with respect to the variable x, using the rules and formulas of differentiation, we obtain what is called the partial derivative of f with respect to x which is denoted by Similarly If we keep x constant and differentiate f (assuming f is




Section 12 3 Partial Derivatives




Partial Derivatives Introduction Video Khan Academy
"partial of w with respect to y; I am asked to show, that f ( x, y) = { x y x 2 − y 2 x 2 y 2 for ( x, y) ≠ ( 0, 0) 0 for ( x, y) = ( 0, 0) is everywhere two times partial differentiable, but it is still D 1 D 2 f ( 0, 0) ≠ D 2 D 1 f ( 0, 0) But this does not make much sense in my opinion Since f ( 0, 0) = 0 hence it should be equal? = ( y^2 z^2 ) / (x^2 y^2 z^2)^(3/2) But I can't for the life of me see where the square root went in the first term of the derivative I see how everything else is simplified, but how does that term suddenly become squared??



Solved Consider The Functions F X Y 4 X 5 Y 2 Y 6 X Y 2 And G X Y X 2 3 X 5 E X Y Find First Order Partial Derivatives X F An Course Hero



Mathweb Math Ncu Edu Tw
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevelPARTIAL DIFFERENTIATION 1 b) wx = −y2/x2, wy = 2y/x;Get the free "Partial derivatives of f(x,y)" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Mathematics widgets in WolframAlpha



1



Ams Sunysb Edu
Therefore at (1,2,4), we get wx = −4, wy = 4, so that the tangent plane is w = 4−4(x −1)4(y −2), or w = −4x 4y x x y 2B2 a) zx = = ;In the second, x, y, z are independent 2 Differentials vs Chain Rule An alternative way of calculating partial derivatives uses total differentials We illustrate with an example, doing it first with the chain rule, then repeating it using differentials BySolve for dy dx;




Doc Chapter Four Derivatives Of Multivariate Functions Partial Differentiation Habtamu Destaw Academia Edu




Multivariate Functions And Partial Derivatives Sage Research Methods
The Derivative Calculator supports solving first, second, fourth derivatives, as well as implicit differentiation and finding the zeros/roots You can also get a better visual and understanding of the function by using our graphing tool Chain Rule d d x f (g (x)) = f ' (g (x)) g ' (x) Step 2 Click the blue arrow to submitY z) The partial derivative of f with respect to x is defined by differentiating f with respect to x, consideri ng y and z as being held constant That is, at a point (x0;What is Second Derivative The second derivative is the derivative of the derivative of a function, when it is defined It makes it possible to measure changes in the rates of change For example, the second derivative of the displacement is the variation of the speed (rate of variation of the displacement), namely the acceleration




Applications Of Partial Derivatives Use The Chain Rule To Find Dz Dt Z X 2 Y 2 Xy X Sin T Y 3e T Wegglab




Partial Derivatives Archives Www Tinspireapps Com Stepwise Math Science Solutions
To find d/dx(sqrt(x^2y^2)), as part of an implicit differentiation problem, use the chain rule d/dx(sqrtx) = 1/(2sqrtx), so d/dx(sqrtu) = 1/(2sqrtu) (du)/dx d/dx(sqrt(x^2y^2)) = 1/(2sqrt(x^2y^2)) * d/dx(x^2y^2) = 1/(2sqrt(x^2y^2))(2x2y dy/dx) =1/(2sqrt(x^2y^2))2x 1/(2sqrt(x^2y^2))2y dy/dx =x/sqrt(x^2y^2) y/sqrt(x^2y^2) dy/dx In order to solve for dy/dxPartial derivative of x/y \square!Answer (1 of 2) The context appears to be classical (Lagrangian) mechanics The overdot is just shorthand for differentiation with respect to time That is, \dot{x}\equiv dx/dt, for instance More importantly, what you are differentiating is the action In Lagrangian physics, the action is tre




Partial Differentiation If Z X Y X 2 Y 2 Show That әz әx әz әy 2 4 1 әz әx әz әy Youtube




Answered Find The Partial Derivatives With Bartleby
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Collect all the dy dx on one side;You first take the partial derivative with respect to x and you get cosine x, y squared Which looks very different from sine x, two y And then when you take the derivative with respect to y, you know, you get a certain value And when you go down the other path, you also get that same value And maybe the way that you write this is that you'd say Let me just copy this guy over here And




Solved Find All The Second Order Partial Derivatives Of The Chegg Com




Consider The Function F X Y Ln X 2 Y 2 3 Compute The Partial Derivatives Of The First And Second Order Mathematics Stack Exchange
If z = f(x,y) = x4y3 8x2y y4 5x, then the partial derivatives are ∂z ∂x = 4x3y3 16xy 5 (Note y fixed, x independent variable, z dependent variable) ∂z ∂y = 3x4y2 8x2 4y3 (Note x fixed, y independent variable, z dependent variable) 2 If z = f(x,y) = (x2 y3)10 ln(x), then the partial derivatives are ∂z ∂x = x(x2 y3)9 1 x (Note We used the chain rule on the firstExample x 2 y 2 = r 2 Differentiate with respect to x d dx (x 2) d dx (y 2) = dDraw graph Edit expression Direct link to this page Value at x= Derivative Calculator computes derivatives of a function with respect to given variable using analytical differentiation and displays a stepbystep solution It allows to draw graphs of the function and its derivatives Calculator
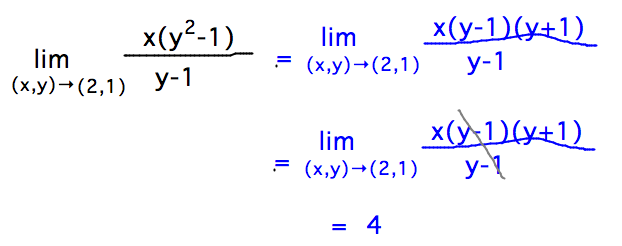



Geneseo Math 223 03 Partial Derivatives
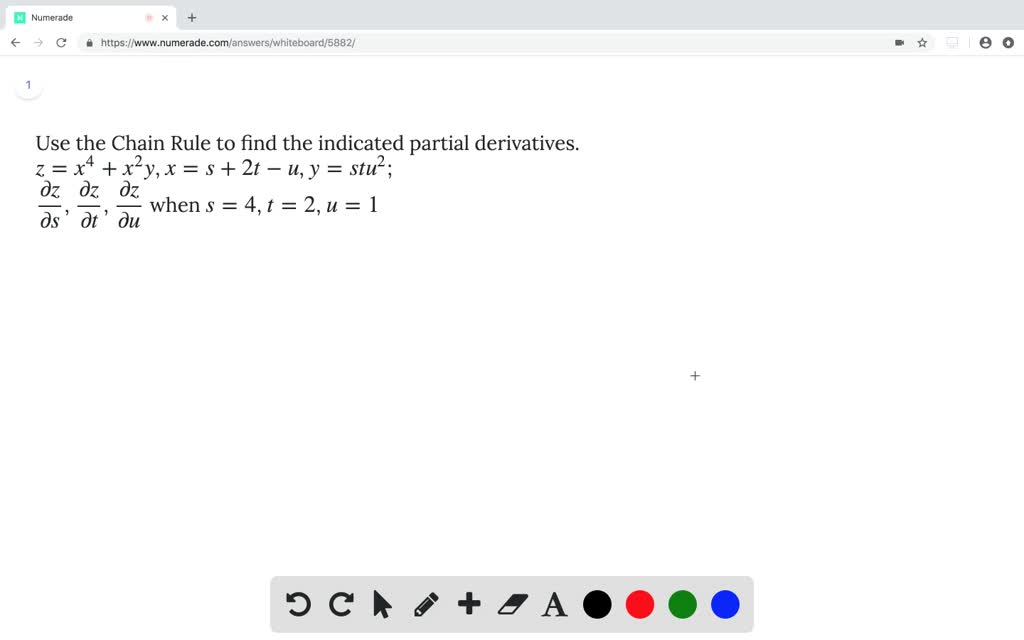



Solved Use The Chain Rule To Find The Indicated Partial Derivatives Z X 4 X 2y X S 2t U Y Stu 2 Dfrac Partial Z Partial S
For the function z = x2y3 Solution z = x2y3 ∴ ∂z ∂x = 2xy3, and ∂z ∂y = x23y2, = 3x2y2 For the first part y3 is treated as a constant and the derivative of x2 with respect to x is 2x For the second part x2 is treated as a constant and the derivative of y3 with respect to is 3 2 Exercise 1 Find ∂z ∂x and ∂z ∂y for each ofPartial derivative of x/ (x^2y^2) \square!Y0 z0) f x0 y0 z0 h Similarly, if we keep x and z constant, we define the partial




Derivative Calculator Wolfram Alpha




Problems On Partial Differentiation U Log X 2 Y 2 Z 2 U Tan 1 2xy X 2 Y 2 Z F X Ay Q X Ay Youtube
Find the partial derivative \(f_x(1,2)\) and relate its value to the sketch you just made Write the trace \(f(1,y)\) at the fixed value \(x=1\text{}\) On the right side of Figure 1025, draw the graph of the trace with \(x=1\) indicating the scale and labels on the axes Also, sketch the tangent line at the point \(y=2\text{}\) Find the partial derivative \(f_y(1,2)\) and relate its value350 Chapter 14 Partial Differentiation this equation into two functions, f(x,y) = p 4− x2 −y2 and f(x,y) = − p 4− x2 −y2, representing the upper and lower hemispheres Each of these is an example of a function with a restricted domain only certain values of x and y make sense (namely, those for which x2 y2 ≤ 4) and the graphs of these functions are limited to a small region ofY = ± √ (r 2 − x 2) x 2 y 2 = r 2 In this form, y is expressed as a function of x In this form, the function is expressed in terms of both y and x The graph of x 2 y 2 = 3 2 How to do Implicit Differentiation Differentiate with respect to x ;




Answered 7 Find The Second Partial Derivatives Bartleby



17 5 Higher Order Partial Derivatives Graphing Calculator By Mathlab User Manual
You will recall that if y= f(x), then the derivative of f, denoted f0(x) or dy dx or d dx f(x) is the instantaneous rate of change of f with respect to x We list some facts about the derivative students should know 1 f0(a) = lim x!a f(x) f(a) x a = lim h!0 f(ah) f(a) h 2If fis di⁄erentiable at a point a( f0(a) exists) then fis continuous at a 3 f0(a) is the slope of the tangent to y



Find The Partial Derivatives Of The Following Functions At The Indicated Points I F X Y 3x 2 2xy Y 2 5x 2 2 5 Sarthaks Econnect Largest Online Education Community



Math Ucla Edu



1



What S The Partial Derivative Of F X Y Log To The Base X Y Quora




Calculus 3 Partial Derivative 14 Of 30 Find More Partial Derivatives Example 2 Of 2 Youtube




Partial Derivative Of F X Y Z With Respect To Z Mathematics Stack Exchange




Higher Derivatives Partial Differentiation



Second Order Partial Derivatives In Calculus



Solved Find All The First And Second Order Partial Derivatives Of F X Y X 2y 2 E Xy Sin X 2y Course Hero




Solved Find The First And Second Order Partial Derivatives Chegg Com




Find The Indicated Partial Derivatives F X Y Ln Left X Quizlet
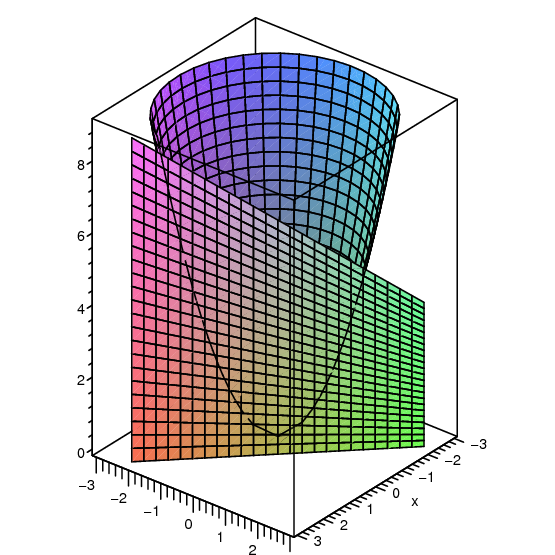



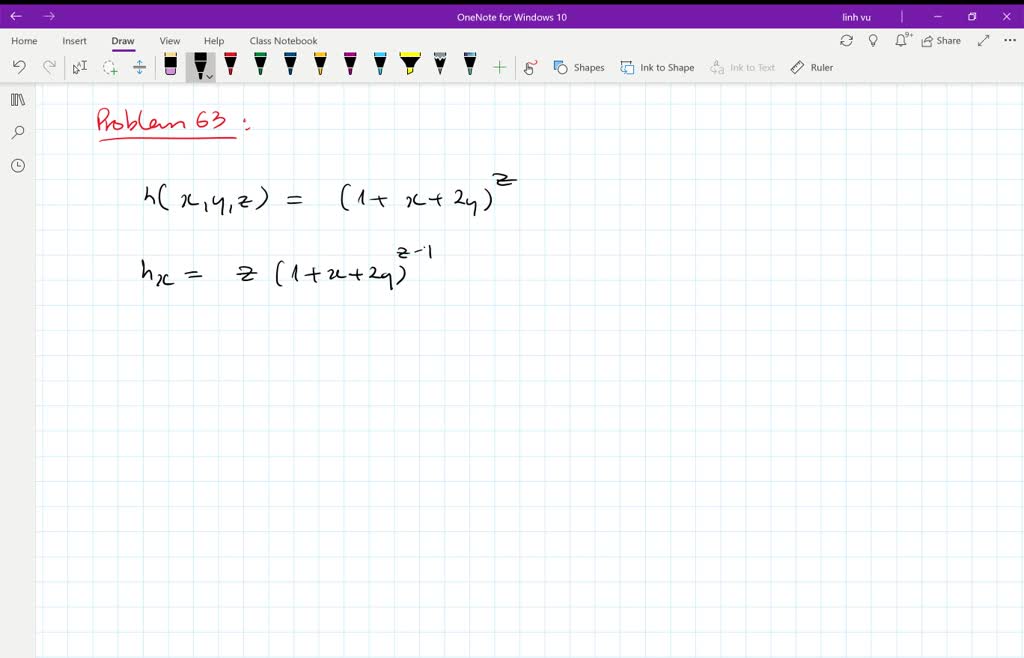
14 3 Partial Differentiation



Link Springer Com




Partial Derivative If U X 2 Tan 1 Y X Y 2 Tan 1 X Y Prove ә 2u әxәy X 2 Y 2 X 2 Y 2 Youtube




Copyright C Cengage Learning All Rights Reserved Partial Derivatives Ppt Download




Derivative Calculator Wolfram Alpha




Pdf Functions Of Several Variables And Partial Di Erentiation 1 Functions Of Several Variables Mic Mus Academia Edu



Partial Derivatives Calculus Volume 3




Copyright C Cengage Learning All Rights Reserved Partial Derivatives Ppt Download



Solved Compute The Second Partial Derivatives For The Following Function F X Y 2xy X2 Y2 2 On The Region Where X Y A 0 0 Aˆ 2f Aˆ X2 Aˆ 2f Aˆ X Aˆ Y Aˆ 2f Aˆ Y Aˆ X Aˆ 2f Aˆ Y2



Math Utoledo Edu




Answered 2 Evaluate The Limit Using The Bartleby



Solved Find All The First And Second Order Partial Derivatives Of F X Y X 2y 2 E Xy Sin X 2y Course Hero




Using Nabla With Partial Derivatives And The Laplace Operation Partial X 2 Partial Y 2 Partial Z 2 Mathematics Stack Exchange




Partial Differentiation And Multiple Integrals Pdf Free Download




Partial Derivative Of Log Detailed Login Instructions Loginnote




Partial F X Y X F X X2 Y2 And Then We Evaluate The Derivative As If Y Is A Constant Pdf Free Download




Partial Derivative Examples Math Insight




Solved Calculate The Second Order Partial Derivatives F X Chegg Com



Rules Of Calculus Multivariate




Solution Find The Partial Derivative With Respect To X Of The Function Xy 2 5y 6




Solved Find All The First Order Partial Derivatives For The Chegg Com




Partial Differentiation



Legacy Www Math Harvard Edu




1 Supplement Partial Derivatives 2 1 D Derivatives Review Given F X F X Df Dx Rate Of Change Of F At Point X W R T X H F X H F X Xx H Ppt Download
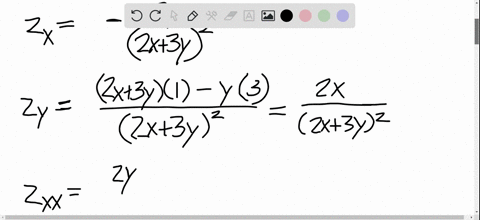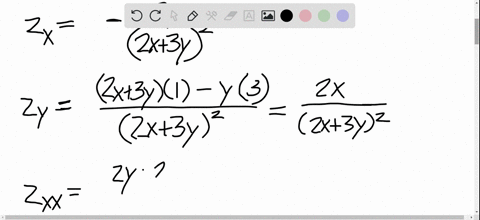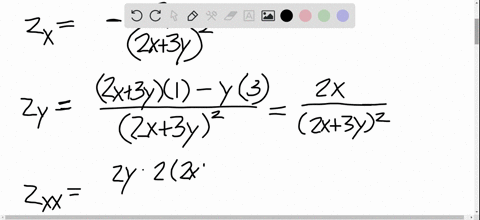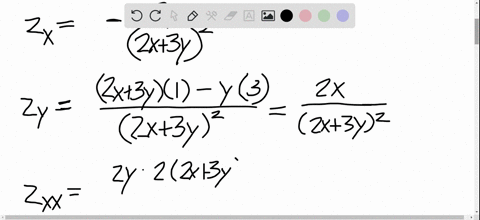



Solved Find All The Second Partial Derivatives Z Dfrac Y 2x 3y




Generalized Second Order Partial Derivatives Of 1 R Iopscience
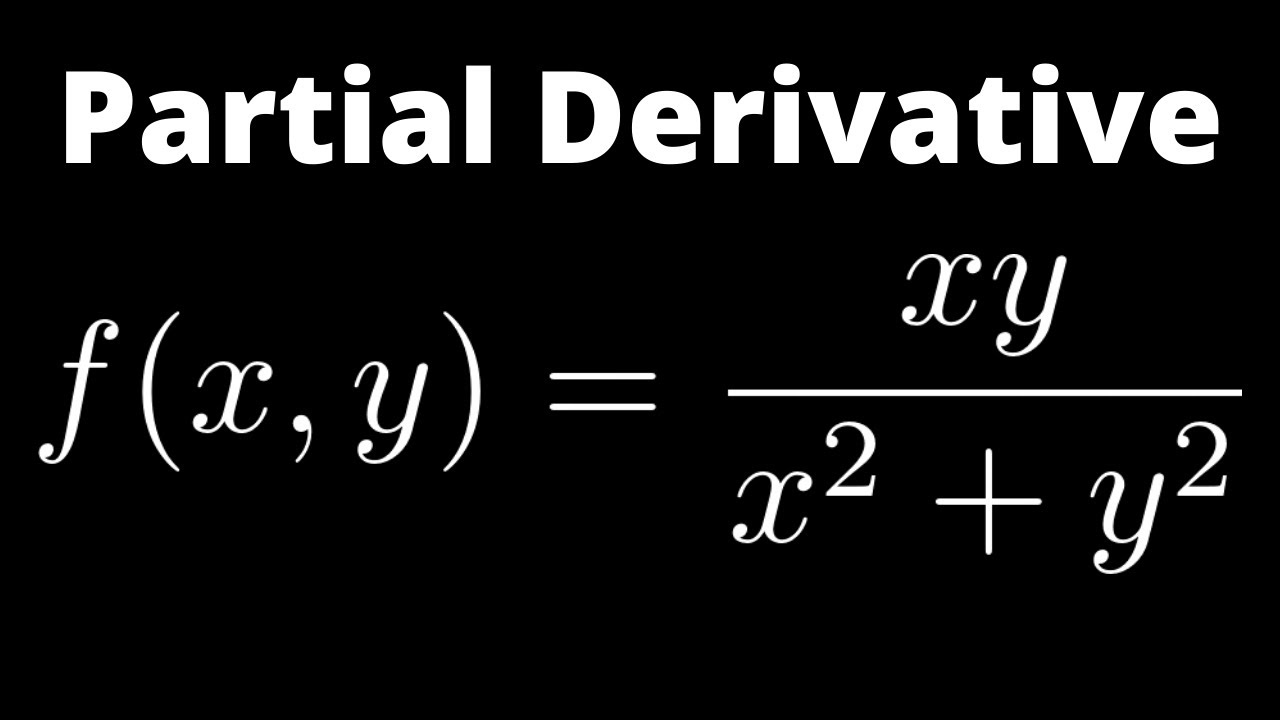



Partial Derivative Of F X Y Xy X 2 Y 2 With Quotient Rule Youtube



Multivariable Partial Derivative Dp




Solved F X Y Z X 2y Y 2z Xz 2 Partial Differential Chegg Com



Abel Math Harvard Edu




Using The Appropriate Properties Of Ordinary Derivatives Perform The Following A Find All The First Partial Derivatives Of The Following Functions F X Y I X 2 Y Ii X 2 Y 2 4 Iii Sin X Y Iv Tan




Second Order Partial Derivatives Ucsd Second



Product Rule




Second Order Partial Derivatives F X Y Sqrt X 2 Y 2 Youtube




Definition Of Partial Derivative Page 128 129 Fx




Partial Differentiation And Multiple Integrals Pdf Free Download



Definition Of Partial Derivative Page 128 129 Fx
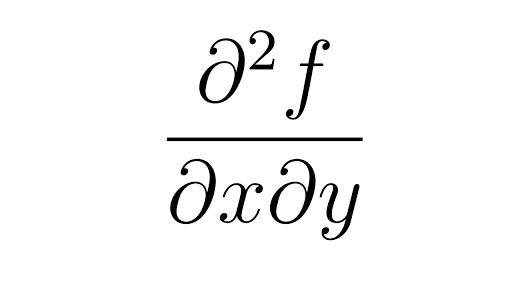



Second Partial Derivatives Article Khan Academy




Show That Xux Yuy Zuz 2u If U X 2 Y 2 Z 2 Partial Derivatives Solved Example Math Traders



Canvas Wpi Edu




Partial Derivative Examples Math Insight




Copyright C Cengage Learning All Rights Reserved Partial Derivatives Ppt Download



What Is The Partial Derivative Of U Y X W R T To X And Y Quora
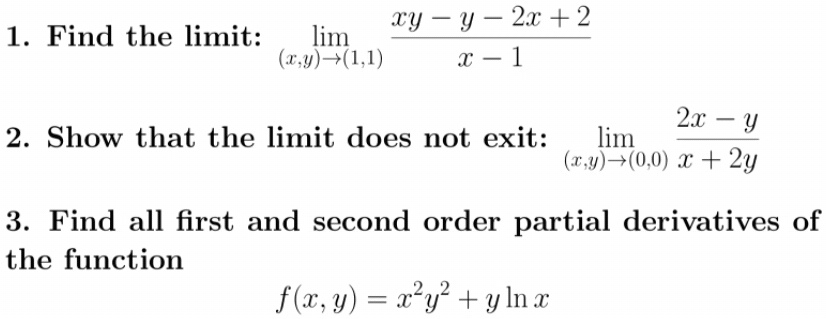



Solved Iy Y 2x 2 1 Find The Limit Lim 1 1 I 1 2x Y 2 Show That The Limit Does Not Exit Lim 0 0 0 X 2y




1 Given F X Y Z As Z 2 Y Find A The Partial Derivative F X Y Homeworklib
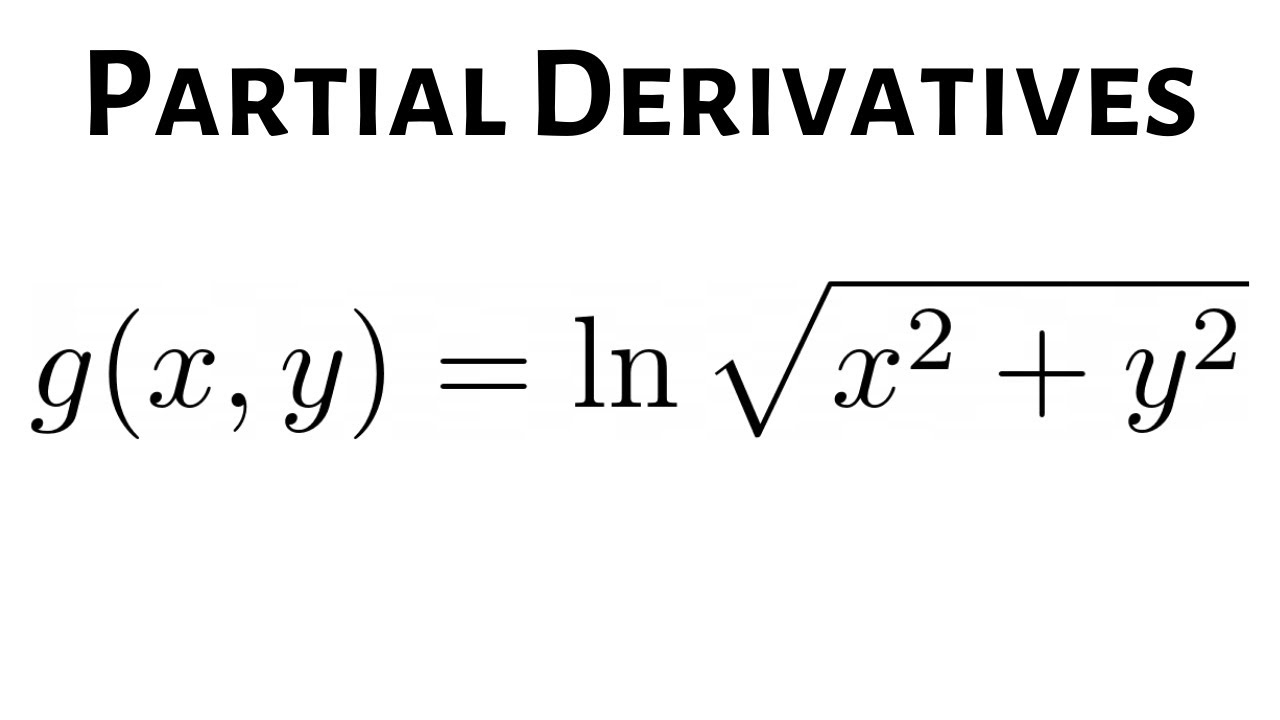



Larson Calculus 13 3 28 First Partial Derivatives Of G X Y Ln Sqrt X 2 Y 2 Youtube



Math Wpi Edu




2 Partial Differentiation
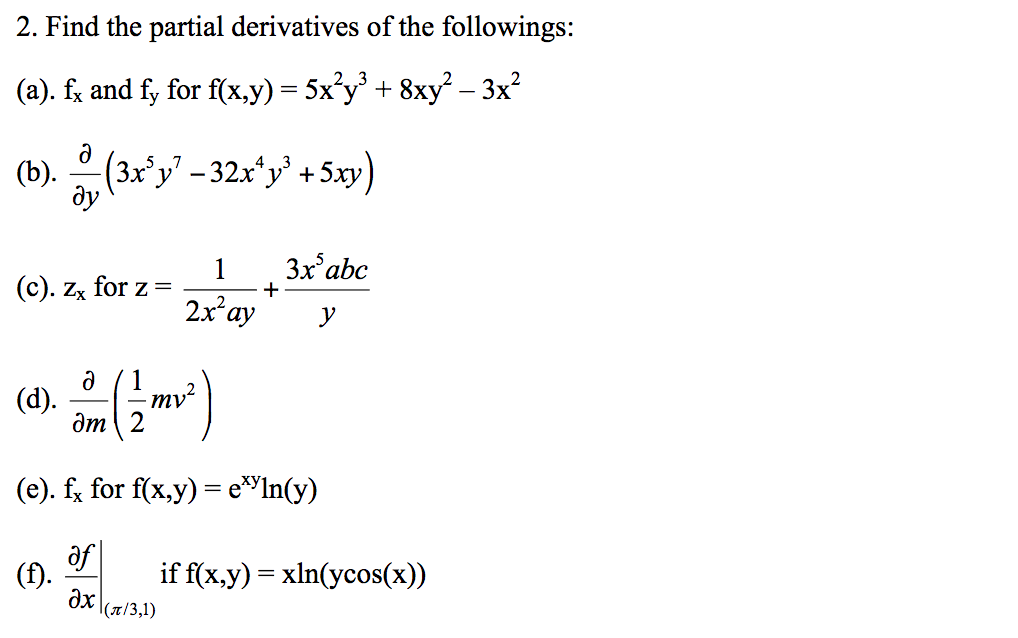



Solved Find The Partial Derivatives Of The Followings F X Chegg Com




Larson Calculus 13 3 26 First Partial Derivatives Of Z Xy X 2 Y 2 Using The Quotient Rule Topic Play



Whitman Edu




Multivariate Functions And Partial Derivatives Sage Research Methods




Partial Differentiation Application Ppt Download



Users Math Msu Edu




1 Partial Derivatives Of F X Y Xy Y Xy Are F Y 2xy Y


